ENCYCLOPEDIA ENTRY

8-Beat Cycle

The fundamental eight-tick recognition cycle from traversing 3D voxel vertices.

Recognition Physics FundamentalsIntermediatecycle, voxel, rhythm

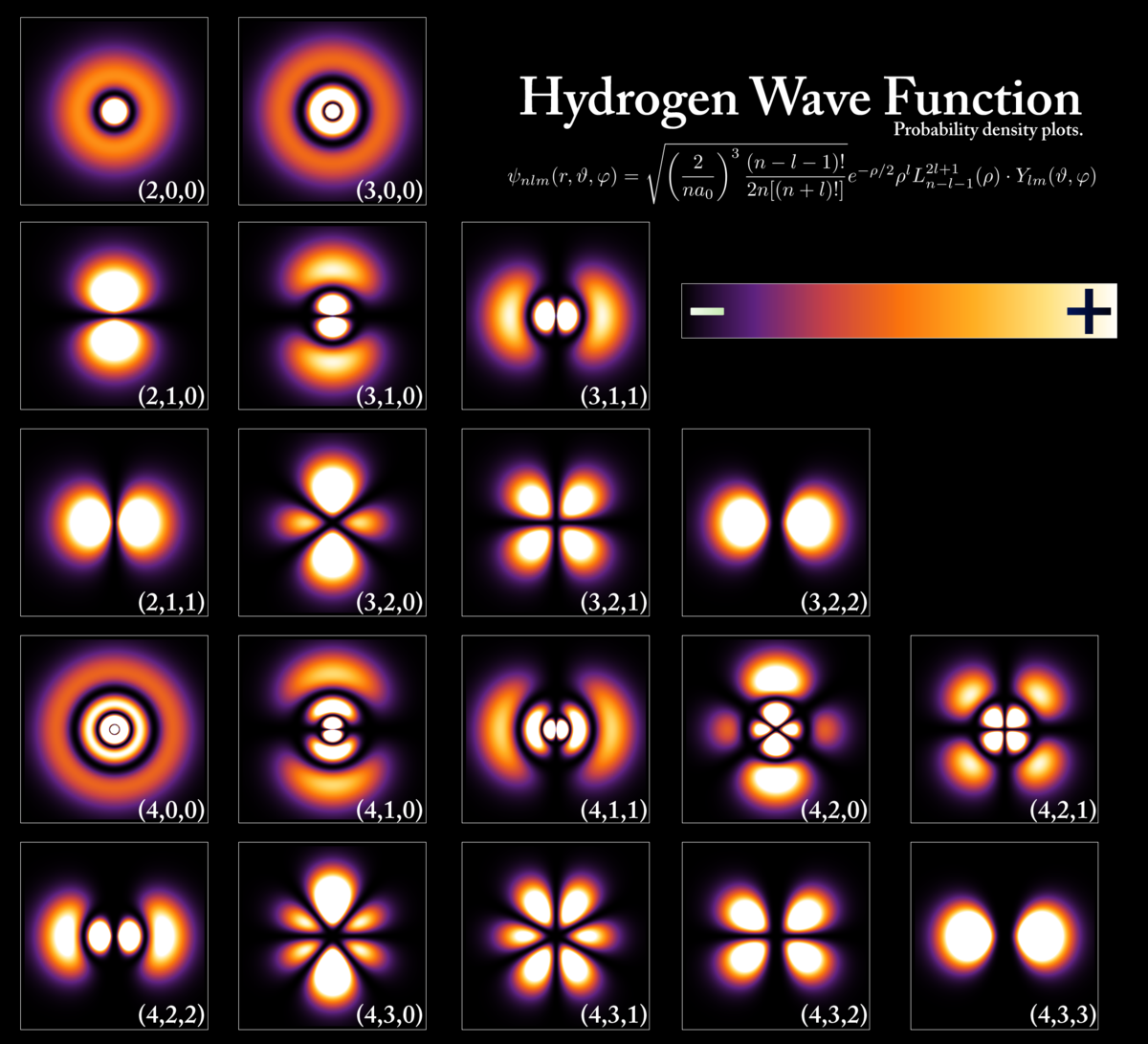
8-Beat Cycle conceptual visualization — Complex patterns emerge from simple recognition rules • Wikimedia Commons • CC BY-SA 3.0

The fundamental eight-tick recognition cycle from traversing 3D voxel vertices.

Essence

The 8-beat cycle is a critical concept in Recognition Science that links the structure of three-dimensional space with the rhythm of time. It represents the minimal temporal period required for a complete recognition of a voxel, which is the fundamental unit of spatial recognition.

Definition

N_{\text{ticks}} = 2^{D_{\text{spatial}}} = 2^3 = 8

In Plain English

Imagine a cube, the simplest three-dimensional shape, made up of eight corners or vertices. To fully recognize this cube in the context of Recognition Science, you need to account for all eight vertices. This process unfolds over eight discrete time steps, or ticks. Each tick corresponds to a fundamental recognition event, ensuring that every vertex is acknowledged. Thus, the 8-beat cycle is not just a number; it is a reflection of the very fabric of our spatial reality.

Why It Matters

The 8-beat cycle establishes a direct relationship between spatial dimensions and temporal cycles. It reveals that the structure of space is inherently tied to the flow of time, suggesting that our universe operates on a rhythm dictated by its geometry. Understanding this cycle is essential for grasping the dynamics of recognition events and the underlying principles of Recognition Science.

How It Works

Feynman diagram showing particle interactions — Recognition events create observable particle interactions • Wikimedia Commons • CC BY-SA 3.0

In a three-dimensional space, each voxel has eight vertices. The recognition of these vertices must occur in a balanced manner to avoid any ledger imbalances. The 8-beat cycle ensures that all vertices are recognized within a single cycle of time, thus maintaining the integrity of the ledger. If fewer than eight ticks were used, some vertices would go unrecognized, leading to an incomplete understanding of the spatial structure.

Key Properties

Completeness: The cycle encompasses all necessary spatial states.
Balance: Ensures that the ledger remains stable and without imbalance.
Universality: The cycle is fundamental to the structure of spacetime itself.

Mathematical Foundation

The number of ticks in the cycle is derived from the relationship between spatial dimensions and temporal cycles:

N_{\text{ticks}} = 2^{D_{\text{spatial}}}\

Connections

The 8-beat cycle is intricately linked to the concept of voxels, as well as the principles of dual-balance and the ledger. It also relates to the broader framework of spacetime and the dynamics of quantum entanglement.

Testable Predictions

One prediction stemming from the 8-beat cycle is that any system operating in a three-dimensional space must exhibit recognition events that conform to this eight-tick structure. This can be tested by observing systems to ensure that they recognize all spatial states within the defined temporal cycle.

Common Misconceptions

A common misconception is that the 8-beat cycle is an arbitrary choice. In reality, it is a necessary consequence of the geometry of three-dimensional space, derived from the fundamental properties of voxels and the requirements of recognition.

FAQs

What is a voxel?

A voxel is the smallest distinguishable unit of 3D space, analogous to a pixel in two dimensions. It is defined by its eight vertices.

Why is the 8-beat cycle important?

The 8-beat cycle is crucial because it ensures that all aspects of a voxel are recognized, maintaining the balance of the ledger and the integrity of the recognition process.